Topic outline

  • Blackbody Radiation - What the Stars tell us

    Collapse all Expand all

    Blackbody curvesBlackbody Radiation and the Stars
    Written by Kathy Gustavson, June 2016
    Grade (Age) Levels: High School (14-18+)
    Topics: Blackbody radiation, Wien's Law, Stefan-Boltzmann Law, dual nature of light.
    This module is a summary of the relation between temperature, energy, and the light emitted by the objects we see in the universe.





    http://sunearthday.gsfc.nasa.gov/2009/images/ttt65_image1.jpg


  • 1. Intro to Thermal Radiation and Blackbodies

    Essential Question for this project: 

    How can we tell the temperature of a star across the vastness of space without visiting the star?

    Intro:
    In the late 1800's, astronomers sought to apply the understanding of the electromagnetic spectrum to objects in the heavens.
    It was understood that different kinds of electromagnetic radiation are produced in different ways. Radio waves are generated by making an electric current oscillate back and forth. X-rays are produced by bombarding a piece of metal with fast moving particles from within other atoms. But what about EM radiation from space? Astronomers started with the simplest and most common way to produce EM radiation on the earth: heat an object.The "thermal" radiation (what we now called infrared radiation), and the visible radiation the hot object emits and absorbs, were studied by scientists, who modeled the object as a "blackbody".  This project will look at this model and its associated laws and apply them to stars. It will also introduce you to the dual nature of light and the birth of quantum physics. 

    Heating an object to glowing:

    Image on Wikipedia: Taken by fir0002 | flagstaffotos.com.au Canon 20D + Tamron 28-75mm f/2.8 - Own work



  • 2. What does Temperature Mean?

    To best understand the relationship between the electromagnetic radiation an object emits and the object's temperature, the meaning of the word "temperature" is important to understand. 
    All matter is composed of continuously moving atoms or molecules. This movement is random and translational (straight line) motion. This motion means that all the particles contained in matter have kinetic energy. We sense the average kinetic energy of all this random motion as temperature. This temperature can be measured with respect to a standard scale.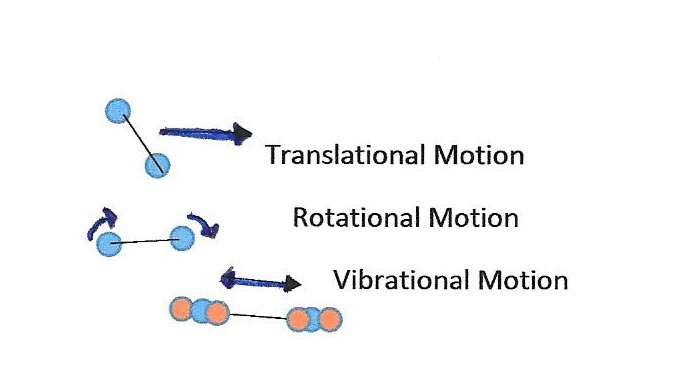

    Temperature is a measure of translational motion only
             
    Note: Temperature measures average translational kinetic energy. Rotational and vibrational motions require more energy and are associated with the specific heat capacity of a substance.

                                        

    Temperature is not the same as heat. Matter does not contain heat. Heat is the energy that flows from one object to another; for example, heat is transferred to your hand or from your hand when you touch a hot stove or an ice cube. Heat changes the total kinetic energy contained in an object by affecting the motion of the molecules. A sparkler has sparks with temperatures in excess of 2000oC, yet, the sparks transfer very little heat to any object they touch.

    Sparkler













    http://sciencenotes.org/wp-content/uploads/2013/05/sparkler.jpg


    Scientists call the total energy contained in matter the internal energy of an object.


    There are three temperature scales  in common use.
    Most of the world uses the Celsius scale (oC), which is based on the behavior of water: water freezes at 0oC and boils at 100oC at sea level on Earth. Scientists, particularly Astronomers, prefer the Kelvin temperature scale. where 0 K is the absolute minimum atomic motion. There are no negative numbers with this scale. (note: we do not use degree (o) with the Kelvin temperature scale.)
    Below is a comparison of the three scales: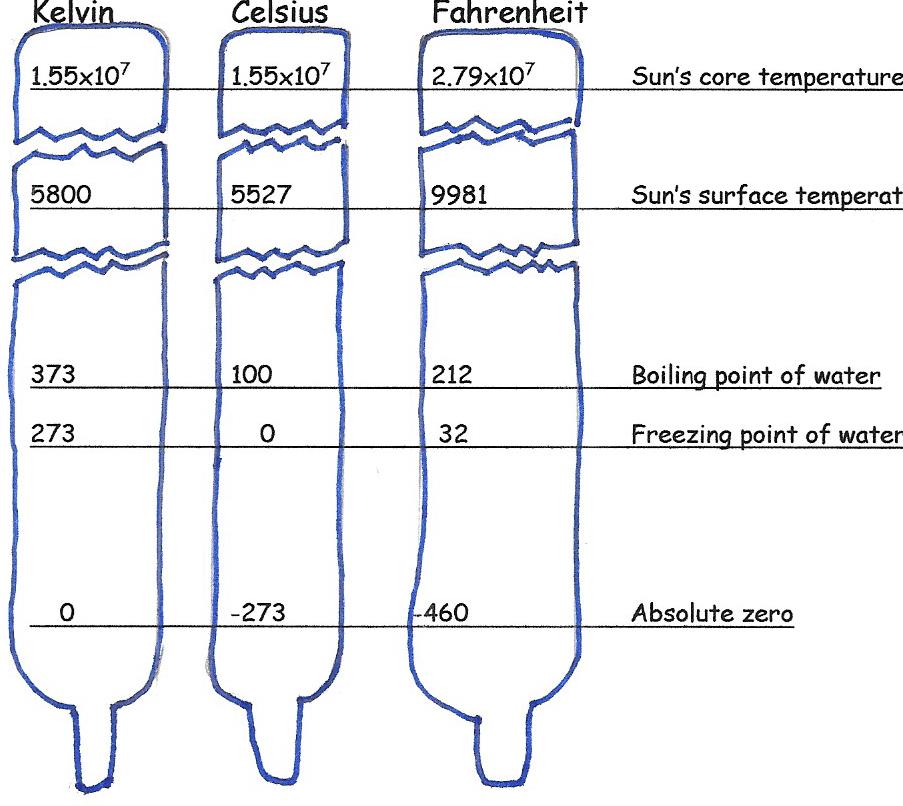


    Comparison of the three scales

  • 3. The Characteristics of a "Blackbody" and Blackbody Curves

    Scientists use the blackbody model to study how hot, dense objects, such as stars or hot coals, emit thermal radiation:
    A blackbody absorbs all incoming light (or any electromagnetic radiation) and converts the light's energy into thermal energy. No electromagnetic radiation is reflected. The energy radiated by the object as EM waves is based solely on its temperature.
    Most objects do reflect light, allowing one to see them. These are not perfect blackbodies. A perfect blackbody at room temperature(around 300 K), appears black to us because the EM radiation it emits is not detectable to our eyes - it is within the infrared range. However, a star appears to behave like a blackbody. It absorbs almost all radiation that falls upon it, causing the electromagnetic radiation emitted to be based only on its temperature. Most stars do not look black because most of the radiation they emit is in the range our eyes detect. 

    The current project you are working on will prepare you for a more advanced, separate project called: Stellar Spectra:Blackbodies or Not?  that will explore just how well the blackbody model works for stars.  

    A sample of blackbody curves and stars

    NASA Image

    To continue the current project, do this simulation: 

    http://astro.unl.edu/classaction/animations/light/meltednail.html

    There should be several things you notice about the simulation: 
    Answer the following questions about this simulation and the curve in Journal 3: Blackbody Curves
    1. What are the labels on each axis? List the units also.
    2. What happens to the curve as the nail is heated?
    3. What happens to the peak wavelength as the nail is heated?
    4. What happens to the area under the curve as the nail is heated?
    5. Come up with one or two questions of you own.

  • 4. Wien's Law for a Blackbody

    In the late 1800s, several physicists studied EM radiation by studying the blackbody model.Two important findings concerned the total power output of a blackbody (Stefan's law) and the wavelength of radiation at which the peak of this power output occurs (Wien's law). This section will look at the equation for each of these law with several examples. 

    Let's return to the very first image in this project: a simple blackbody curve (the curve is also referred to as a "Planck" curve: we will discuss Maxwell Planck later).

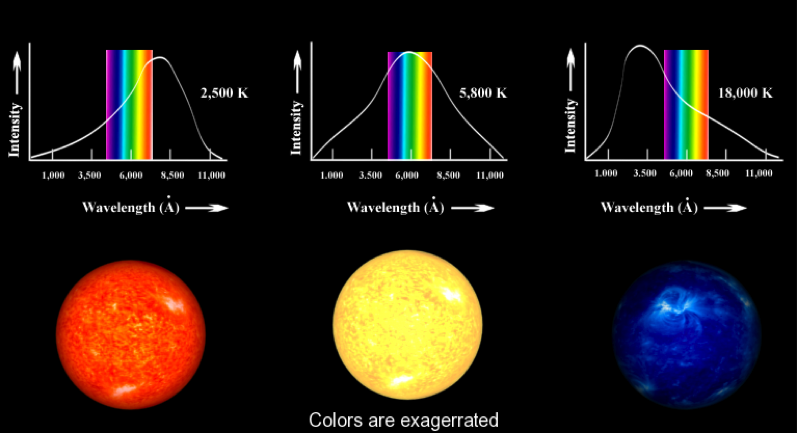
    Planck CurvesThese four curves show how much radiation is emitted by a dense object (idealized) at each wavelength on the electromagnetic spectrum. The vertical scale is intensity and the horizontal scale is wavelength, in this case, nanometers (10-9meters). 




    Using Journal 4, answer these general questions about the above curves:

    a.) What would the curve look like if the object radiated the same energy intensity for every wavelength?
    b.) How does the shape of the curve change for each temperature?
    c.) What color would each of these objects appear to us?
    d.) How can this be applied to stars? What would we need to measure? Do stars actually appear different colors?

    Wien's Law  finds Temperature:

    T = 2,897,000 nm-K/λmax(nm)
    where the λ is wavelength in nanometers (10-9 meters), and T is temperature in Kelvins.

    Example Exercise 1: The surface temperature of the Sun
    The maximum power per wavelength of radiation from the Sun is at a wavelength of 510 nm. This appears to our eyes as yellow light. What is the surface temperature of the Sun?

    Solve and evaluate using Wien's law:

           T =( 2,897,000 nm-K)/510 nm = 5680 K

    This is about the temperature of the object in the above figure with the highest intensity (the uppermost curve). At this temperature, matter is in a gaseous state, but the Sun's huge mass, and thus, huge gravitational field prevents the gaseous matter from easily leaving.

    Let's return to a previous image: 
    These blackbody curves have the visible spectrum added.
    Answer these question in Journal 4:
    a.)The leftmost curve peaks at what color? Are there other colors present in the light being emitted from the star? Why does it appear reddish orange? Is it a cool or hot star?
    b.)The middle spectrum is similar to the sun. What is its peak color? Why is it not white? Is it cooler or hotter than the leftmost star?
    c.) Discuss the rightmost star in terms of temperature, and color. Should we be able to see it?


    Problem 1: (Try it yourself- show the work in Journal 4)

    The surface temperature of Earth is about 288 K. What is the peak intensity wavelength of maximum radiation by the Earth?

          (did you get 10,000 nm? Where is this on the electromagnetic spectrum?)


  • 5. Stefan-Boltzmann Law

    Stefan-Boltzmann law:Total Power Output

    The amount of energy emitted by a blackbody depends both on its temperature and on its surface area. A burning match can have the same temperature as a burning log, but the surface areas are vastly different: the burning log radiates far more energy.

    burning match

    burning log

    It is convenient to look at the amount of energy emitted from each square meter of an object per second. This quantity is called the energy flux (F). Flux means "rate of flow" and energy flux means rate of flow of energy. It is measured in joules per square meter per second. A joule is a unit of energy in the metric system (like a calorie), and a watt is a joule per second (so a 40 watt light bulb uses 40 joules of energy per second).
    The equation is:
                   F = σT4

      where F = energy flux, in joules per square meter of surface per second
                  σ = a constant = 5.67 x 10-8W m-2K-4
                         T = object's temperature, in kelvins

    Example Exercise 2:
    What is the energy flux at the Sun's surface? Use the temperature found in Example 1 in the above section.
            Use the above equation with T = 5680K.
    The result is: Flux = 5.9 x 107 Watts/square meter. 

    Problem 2: You try it:
    Given the Sun's radius of 6.96 x 108 meters, find the total energy output of the Sun in one second (your answer will be in Watts). Show your work in Journal 5.


  • 6. The Ultraviolet Catastrophe and the Dual Nature of Light

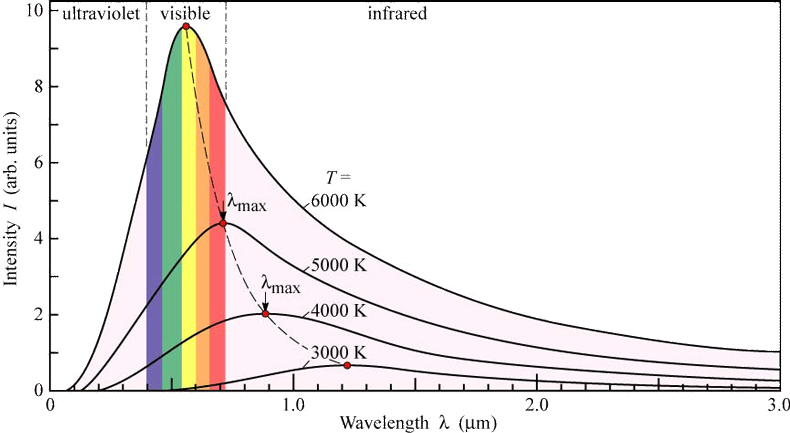
    By the late 1800's, the study of blackbody radiation helped in developing a model to explain how objects emit electromagnetic radiation: Atoms and molecules are made of charged particles, and when these particles vibrate, they radiate electromagnetic waves. And furthermore, the higher the frequency of the vibration, the higher the frequency of emitted electromagnetic waves. The atoms and molecules in blackbodies vibrate at many different frequencies, all centered around the peak frequency found on spectrum curve for that blackbody. The electromagnetic wave theory developed by James Maxwell predicted that the intensity of radiation emitted by a blackbody should increase with the frequency of the radiation - shorter wavelengths give rise to higher intensities. But actual spectral curves show that at high frequencies (short wavelengths), the emitted intensity actually drops off. Look at the diagram below:

    Blackbody curve and the ultraviolet catrastropheAnswer these questions in Journal 6:
    a.) As the wavelength gets shorter, what happens to the left side of the curve?
    b.) What does the classical theory predict for a 5000 K object?

    This became know as the Ultraviolet Catastrophe

    Image: wikipedia

    Max Planck worked on this problem for several years. He devised a model that predicted the correct spectral curve for blackbodies. He came up with a model that still had vibrating charged particles inside objects produce electromagnetic radiation, but, if they radiate only in discrete quantities, (one portion is called one quantum), than a mathematical function could describe the actual blackbody curve. He proposed that each oscillating charged particle had a fundamental portion of energy that was proportional to its frequency of oscillation, and that the particle could then emit amounts of energy equal only to multiples of this fundamental portion of energy. This idea is known as Planck's hypothesis.
    After he derived the function for the blackbody curve, he was able to match the calculated and experimental values to find a constant of proportionality, and therefore, a simple equation to relate the energy of this portion of energy to the frequency of oscillation:
                            E = hf
               where E = energy
                            h = Planck's constant (see below for the value)
                            f = frequency of the oscillating charged particle in Hertz
    This equation can be rewritten in terms of wavelength:
                           E = hc/λ
               where E = energy
                           h = Planck's constant
                           c = speed of light (same for all electromagnetic waves: 3 x 108 m/s)
                           λ = wavelength in meters

    This idea of electromagnetic energy emitted in discrete portions implied a new view of the nature of light. These discrete packages of energy are now called "photons". The energy of each photon is related to the wavelength of the electromagnetic wave associated with it. The shorter wavelengths have higher energies, and the longer wavelengths have lower energies. Planck's work supported the idea that light has a dual nature - both wave and particle. It was a difficult concept for scientists to accept. Even now, the image this dual nature evokes is varied. Two representations are shown here: One can be thought of as packets of energy with a wave nature, or a wave with packets of energy.






    Planck's constant is a very small number, 6.625 x 10-34 Joules-second. Hence, the amount of energy is very small. A  single photon of red light, for example, with a wavelength of 633 nm, has an energy of 3.14 x 10-19 J (see example exercise 3 below). This energy is so small that it is sometimes expressed in a different unit - the electron volt (eV). 

                         1 eV = 1.602 x 10-19 J, so the 633 nm photon has an energy of 1.96 eV. 

    Example Exercise 3:
    One can think of a beam of light as a stream of tiny packets of energy now called photons. The scanners used at supermarkets and other stores emit orange-red light of wavelength 633 nm. A nanometer (nm) is equal to 10-9 meters:

                               λ = (633 nm) (10-9 m/1 nm) = 6.33 x 10-7 m
    Then, using Planck's formula, E = hc/λ, we find that

                               E =  (6.625 x 10-34 J s)(3 x 108 m/s)/ 6.33 x 10-7 m = 3.14 x 10-19 J
    This is a very small amount of energy. How many photons does the laser bar code scanner emit per second? If the total energy emitted is typically 1 x 10-3 J, then:
                                             (1 x 10-3 Joules per second)/ (3.14 x 10-19 Joules per photon) = 3.2 x 1015 photons per second
    This large number makes the laser beam seem like a continuous flow of energy, and not like a stream of particles.

    Problem 3: You try it:
    What is the energy contained in a photon of ultraviolet light, specifically, the short UV radiation used in UVB Tanning beds. Use 300 nm as the wavelength. to find this energy. Why are UVB photons more dangerous than UVA photons?
    Use Journal 6 to record you work and answers.                   

    Max Planck thought of the quantization of energy as a mathematical trick. He had a lot of doubts as to whether matter could really behave in discrete energy portions. He knew standing waves could, but matter? A few scientists, including Einstein, applied his ideas to explain other phenomena, and thus today, Planck's quantum model is considered the birth of quantum physics.
    There are several videos below that summarize part of this section. For at least one of the videos, write a few sentences or notes in Journal 6. 

  • Reflection and Course Feedback

    Please let us know your thoughts about this course by using the discussion forum below

    • What was your favorite activity? 
    • What was the most important part of the course for you? 
    • Are there any areas that need improvement? 
    • How was the length of the course? 
    • Any additional comments
    Please use complete sentences in your responses. 


    After you use the discussion forum, please answer the BRIEF survey questions in the link below.

    Thank You!!!